力扣刷题

基础知识

1 数据结构简介

  • 线性数据结构
    • 数组
    • 链表：
    • 栈：LinkedList
      • addLast(E e)、removeLast()
    • 队列：Queue
      • offer(E e)、poll()
  • 非线性数据结构
    • 树
    • 堆
    • 散列表
    • 图

2 stream 流处理

  • 中间处理
    • filter()
    • limit()
  • 最终处理
    • forEach()
    • count()
    • collect()
1
2
3
4
5
Arrays.stream(new int[]{...}).max().getAsInt(); // 获取int数组最大值

// 获取List<Node>中 node.val > 123的 100 个数据
List<Node> list2 = list.stream().filter(a -> a.val > 123).limit(100).collect(Collectors.toList());

解题

一 链表

1 图书整理Ⅰ

书店店员有一张链表形式的书单，每个节点代表一本书，节点中的值表示书的编号。为更方便整理书架，店员需要将书单倒过来排列，就可以从最后一本书开始整理，逐一将书放回到书架上。请倒序返回这个书单链表。

1
2
3
输入：head = [3,6,4,1]

输出：[1,4,6,3]

  • 法1：计算长度，然后插入

  • 法2：先正向遍历，插入栈中，然后一个一个出栈

  • 法3：递归：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    class Solution {
        int[] res;
        int i = 0;
        int j = 0;
        public int[] reversePrint(ListNode head) {
            solve(head);
            return res;
        }
        public void solve(ListNode head){
            if(head == null){
                res = new int[i];
                return;
            }
            i++; 
            solve(head.next);
            res[j] = head.val;
            j++;
        }
    }

2 反转链表

  • 双指针

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    class Solution {
        public ListNode trainningPlan(ListNode head) {
            ListNode cur = head, pre = null;
            while(cur != null) {
                ListNode tmp = cur.next; // 暂存后继节点 cur.next
                cur.next = pre;          // 修改 next 引用指向
                pre = cur;               // pre 暂存 cur
                cur = tmp;               // cur 访问下一节点
            }
            return pre;
        }
    }

  • 递归

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    class Solution {
        public ListNode trainningPlan(ListNode head) {
            return recur(head, null);    // 调用递归并返回
        }
        private ListNode recur(ListNode cur, ListNode pre) {
            if (cur == null) return pre; // 终止条件
            ListNode res = recur(cur.next, cur);  // 递归后继节点
            cur.next = pre;              // 修改节点引用指向
            return res;                  // 返回反转链表的头节点
        }
    }

  • k个一组反转链表，不足k个就保持原序

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    // 主要是找出四个节点：pre, left, right, post 然后反转[left, right]，最后接上left.next和pre.next
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;

        ListNode pre = dummy; // 反转左端点左侧
        ListNode right = dummy; // 反转右端点

        while(right.next != null) {
            for (int i = 0; i < k && right != null; i++) {
                right = right.next;
            }

            if(right == null) break;

            ListNode left = pre.next; // 反转左端点
            ListNode post = right.next; // 反转右端点右侧

            right.next = null;
            pre.next = reverse(left);

            left.next = post;
            pre = left;

            right = pre;
        }
        return dummy.next;
    }

    // 反转单一链表
    private ListNode reverse(ListNode node) {
        ListNode pre = null;
        ListNode cur = node;
        
        while(cur != null) {
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }

3 链表中倒数第k个

  • 快慢指针：先让快指针前进k步，然后一起前进直到fast指针到null

4 合并链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public ListNode trainningPlan(ListNode l1, ListNode l2) {
        ListNode dum = new ListNode(0), cur = dum;
        while(l1 != null && l2 != null) {
            if(l1.val < l2.val) {
                cur.next = l1;
                l1 = l1.next;
            }
            else {
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        cur.next = l1 != null ? l1 : l2;
        return dum.next;
    }
}

5 寻找链表公共节点

  • 快慢指针：先让长的链表先走k步，然后一起走

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    public class Solution {
        public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
            int lena = 0, lenb = 0;
            ListNode a = headA, b = headB;

            while(a != null){
                lena++;
                a = a.next;
            }

            while(b != null){
                lenb++;
                b = b.next;
            }

            int d = lena - lenb;

            if(d > 0){
                while(d-- > 0)
                    headA = headA.next;
            }else if(d < 0){
                d = -d;
                while(d-- > 0)
                    headB = headB.next;
            }

            while(headA != headB){
                headA = headA.next;
                headB = headB.next;
            }
            return headA;
        }
    }

  • 循环指针：两个指针分别先走自己的链表，再走另一条链表，如果有公共节点，则会再某一时刻相同

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    public class Solution {
        public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
            ListNode A = headA, B = headB;
            while (A != B) {
                A = A != null ? A.next : headB;
                B = B != null ? B.next : headA;
            }
            return A;
        }
    }

6 随机链表的复制

  • 方式一：使用map：第一遍构造原node和新node的对应关系，第二遍构造原node的next和random指针和新node的next和random指针的关系

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    class Solution {
        public Node copyRandomList(Node head) {
            if(head == null) return null;
            Node cur = head;
            Map<Node, Node> map = new HashMap<>();
            // 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
            while(cur != null) {
                map.put(cur, new Node(cur.val));
                cur = cur.next;
            }
            cur = head;
            // 4. 构建新链表的 next 和 random 指向
            while(cur != null) {
                map.get(cur).next = map.get(cur.next);
                map.get(cur).random = map.get(cur.random);
                cur = cur.next;
            }
            // 5. 返回新链表的头节点
            return map.get(head);
        }
    }

  • 方式二：考虑构建 原节点 1 -> 新节点 1 -> 原节点 2 -> 新节点 2 -> …… 的拼接链表，如此便可在访问原节点的 random 指向节点的同时找到新对应新节点的 random 指向节点。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    class Solution {
        public Node copyRandomList(Node head) {
            if(head == null) return null;
            Node cur = head;
            // 1. 复制各节点，并构建拼接链表
            while(cur != null) {
                Node tmp = new Node(cur.val);
                tmp.next = cur.next;
                cur.next = tmp;
                cur = tmp.next;
            }
            // 2. 构建各新节点的 random 指向
            cur = head;
            while(cur != null) {
                if(cur.random != null)
                    cur.next.random = cur.random.next;
                cur = cur.next.next;
            }
            // 3. 拆分两链表
            cur = head.next;
            Node pre = head, res = head.next;
            while(cur.next != null) {
                pre.next = pre.next.next;
                cur.next = cur.next.next;
                pre = pre.next;
                cur = cur.next;
            }
            pre.next = null; // 单独处理原链表尾节点
            return res;      // 返回新链表头节点
        }
    }

7 归并排序

  • 给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表

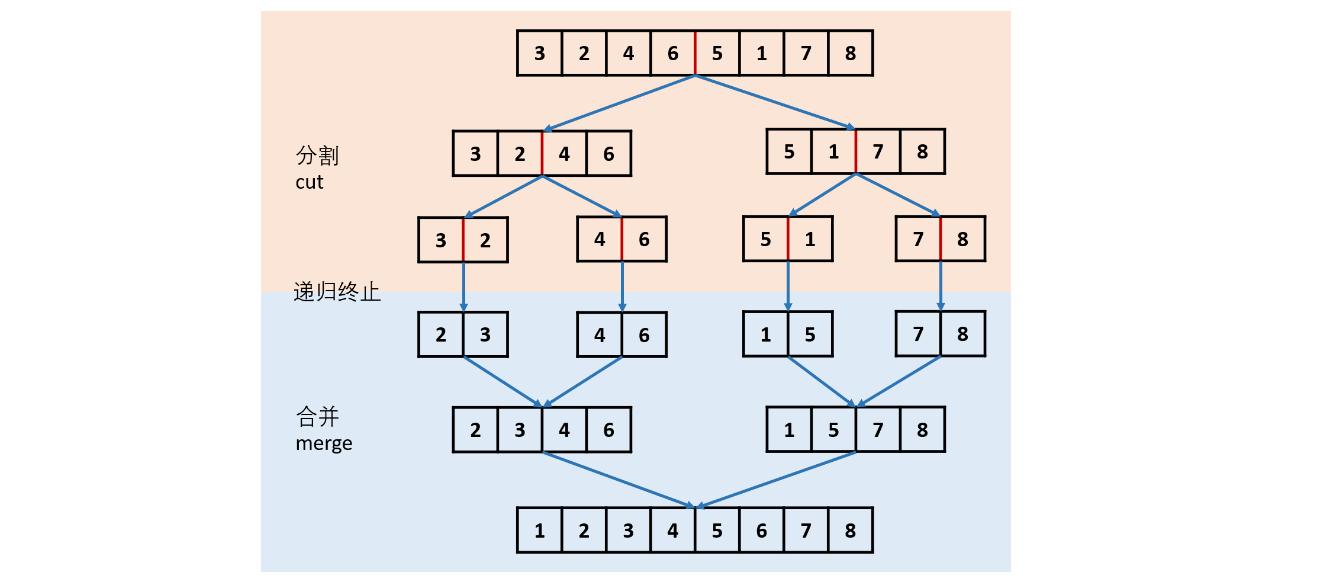
image-20240630221715150

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public ListNode sortList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    // 找到中点
    ListNode fast = head.next, slow = head;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }

    ListNode temp = slow.next;
    slow.next = null;
    ListNode left = sortList(head);
    ListNode right = sortList(temp);

    ListNode h = new ListNode(0);
    ListNode res = h;

    while (left != null && right != null) {
        if (left.val < right.val) {
            h.next = left;
            left = left.next;
        } else {
            h.next = right;
            right = right.next;
        }
        h = h.next;
    }
    h.next = left != null ? left : right;
    return res.next;        
}

8 合并k个升序链表

  • 法1：优先级队列

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    public ListNode mergeKLists(ListNode[] lists) {
        PriorityQueue<ListNode> queue = new PriorityQueue<>(new Comparator<ListNode>() {
            public int compare(ListNode node1, ListNode node2) {
                return node1.val - node2.val;
            }
        });

        for (ListNode node : lists) {
            if (node != null) {
                queue.offer(node);
            }
        }

        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;

        while (!queue.isEmpty()) {
            ListNode node = queue.poll();
            cur.next = node;
            cur = cur.next;

            if (node.next != null) {
                queue.offer(node.next);
            }
        }

        return dummy.next;
    }

  • 法2：分治合并

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    class Solution {
        public ListNode mergeKLists(ListNode[] lists) {
            return merge(lists, 0, lists.length - 1);
        }

        private ListNode merge(ListNode[] lists, int l, int r) {
            if (l == r) {
                return lists[l];
            }

            if (l > r) {
                return null;
            }
            int mid = (l + r) >> 1;
    		// 分
            return merge2Lists(merge(lists, l, mid), merge(lists, mid+1, r));
        }

        // 治
        private ListNode merge2Lists(ListNode node1, ListNode node2) {
            if (node1 == null || node2 == null) {
                return node1 == null ? node2 : node1;
            }

            ListNode dummy = new ListNode();
            ListNode cur = dummy;
            ListNode node1Temp = node1;
            ListNode node2Temp = node2;

            while (node1Temp != null && node2Temp != null) {
                if (node1Temp.val < node2Temp.val) {
                    cur.next = node1Temp;
                    node1Temp = node1Temp.next;
                } else {
                    cur.next = node2Temp;
                    node2Temp = node2Temp.next;
                }
                cur = cur.next;
            }

            cur.next = node1Temp == null ? node2Temp : node1Temp;

            return dummy.next;
        }
    }

二 数组

  • 双指针:前后夹击

  • 滑动窗口:一前一后

  • 和为k的子数组

    • 方法一：前缀和+暴力O(n2)

    • 方法二：前缀和+哈希表O(n)

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      // key：前缀和，value：key 对应的前缀和的个数
      Map<Integer, Integer> preSumFreq = new HashMap<>();
      // 对于下标为 0 的元素，前缀和为 0，个数为 1
      preSumFreq.put(0, 1);

      int preSum = 0;
      int count = 0;
      for (int num : nums) {
          preSum += num;

          // 先获得前缀和为 preSum - k 的个数，加到计数变量里
          if (preSumFreq.containsKey(preSum - k)) {
              count += preSumFreq.get(preSum - k);
          }

          // 然后维护 preSumFreq 的定义
          preSumFreq.put(preSum, preSumFreq.getOrDefault(preSum, 0) + 1);
      }
      return count;

  • 寻找数组中的众数（一定存在）

    • 哈希表

    • 排序，然后中间的就是众数

    • Boyer-Moore 投票算法

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      public int majorityElement(int[] nums) {
          if(nums.length == 0) {
              return -1;
          }

          int temp = nums[0];
          int count = 1;
          for(int i = 1; i < nums.length - 1; i++) {
              if(nums[i] == temp) {
                  count++;
              }else {
                  count--;
                  if(count == 0) {
                      // 因为一定存在众数，所以count = 0时i一定不是最后一个
                      temp = nums[++i];
                      count++;
                  }
              }
          }

          return temp;
      }

2.1 股票问题

  • 动态规划

  • 只能买卖一次

    • dp[i]表示第i天所能获得的最大利润
    • 动态维护一个最小价格minPrice
    • dp[i] = max(dp[i-1], price[i] - minPrice)

  • 可以多次买卖，同一时刻最多持有一股

    • dp[i][j]，j表示状态0为没有股票，1表示持有股票，表示第i天的利润。
    • dp[0][1] = -price[0]
    • 状态转移
      • dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) 维持前一天状态or当天卖掉
      • dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]) 维持前一天状态or当天买入

  • 可以完成两次买卖，同一时刻最多持有一股

    • 状态说明
      • 未进行操作，利润为0，可以不记录
      • 只买了一次 buy1
      • 买一次和卖一次 sell1
      • 买两次和卖一次 buy2
      • 买两次和卖两次 sell2
    • 初始状态
      • buy1 = buy2 = -prices[0]
      • sell1= sell2 = 0
    • 状态转移
      • buy1 = Math.max(buy1, -prices[i]);
      • sell1 = Math.max(sell1, buy1 + prices[i]);
      • buy2 = Math.max(buy2, sell1 - prices[i]);
      • sell2 = Math.max(sell2, buy2 + prices[i]);

  • 可以完成k次买卖，同一时刻最多持有一股

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    public int maxProfit(int k, int[] prices) {
        int n = prices.length;
    	// 1 定义
        // buy[i][j] 第i天进行了j笔交易且还有股票的情况下的最大利润
        // sell[i][j] 第i天进行了j笔交易且没有股票的情况下的最大利润
        int[][] buy = new int[n][k+1];
        int[][] sell = new int[n][k+1];

        // 2 初始状态：初始化 第一行和第一列
        // 2.1 只买一股但是不卖： buy[0:n-1][0] = -prices[0]
        // 2.2 第1天最多操作一次：buy[0][1:k] 、sell[0][1:k]
        buy[0][0] = -prices[0];
    	
        // buy[1:n-1][0] sell[1:n-1][0]
        for (int i = 1; i < n; i++) {
            buy[i][0] = Math.max(buy[i-1][0], -prices[i]);
            // sell[i][0] = 0;
        }
        
    	// buy[0][1:k] sell[0][1:k]
        for(int j = 1; j <= k; j++) {
            // 没有意义的数据：第一次不可能完成一次完整交易, /2是为了防止数据溢出
            buy[0][j] = Integer.MIN_VALUE / 2;
            sell[0][j] = Integer.MIN_VALUE / 2;
        }

        // 3 状态转移
        for(int i = 1; i < n; i++) {
            for(int j = 1; j <= k; j++) {
                // 第i天持股且完成了j次交易：由i-1天持股状态变来 or i-1天不持股但是第i天买入
                buy[i][j] = Math.max(buy[i-1][j], sell[i-1][j] - prices[i]);
                
                // 第i天不持股完成了j次交易：由i-1天不持股状态变来 or i-1天持股但是第i天卖出
                sell[i][j] = Math.max(sell[i-1][j], buy[i-1][j-1] + prices[i]);
            }
        }
    	
        // 4 返回sell[n-1]中最大的一个，分别对应完成了k次交易后的最大收益
        return Arrays.stream(sell[n - 1]).max().getAsInt();
    }

2.2 吃橘子(记忆存储dp)

  • 厨房里总共有 n 个橘子，你决定每一天选择如下方式之一吃这些橘子：

    • 吃1个
    • 吃1/2 前提是n被2整除
    • 吃2/3 前提是n被3整除

    返回吃掉所有橘子最小的天数

  • 法1：动态规划，int[] dp = new int[n]，时间复杂度O(n)

  • 法2：记忆存储，不一个一个的遍历

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    Map<Integer, Integer> memo = new HashMap<Integer, Integer>();
    public int minDays(int n) {

        if(n <= 1) {
            return n;
        }

        if(memo.containsKey(n)) {
            return memo.get(n);
        }

        memo.put(n, Math.min(n % 2 + 1 + minDays(n / 2), n % 3 + 1 + minDays(n / 3)));

        return memo.get(n);
    }

2.3 矩阵中最大得分(二维前缀和)

  • 给一个二维矩阵，求出其中的一个子矩阵(至少包含两个单元)，使其右下角-左上角的值最大

    二维前缀和+动态规划

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    public int maxScore(List<List<Integer>> grid) {
        int ans = Integer.MIN_VALUE;
        int m = grid.size()
        int n = grid.get(0).size();
    	// f[i+1][j+1]表示矩阵左上角[0,0]，右下角[i,j]的子矩阵的最小值
        // f[i+1][j+1] = min(f[i+1][j], f[i][j+1], grid[i][j])
        int[][] f = new int[m + 1][n + 1];
        Arrays.fill(f[0], Integer.MAX_VALUE);

        for (int i = 0; i < m; i++) {
            f[i + 1][0] = Integer.MAX_VALUE;
            for (int j = 0; j < n; j++) {
                int mn = Math.min(f[i + 1][j], f[i][j + 1]); // 上面和左边拿小的那个
                int x = grid.get(i).get(j);
                ans = Math.max(ans, x - mn);
                f[i + 1][j + 1] = Math.min(mn, x);
            }
        }
        return ans;
    }

2.4 数组合并问题

  • 关键是先将数组的左端点或者右端点按照大小排序

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    Arrays.sort(points, new Comparator<int[]>() {
        public int compare(int[] a, int[] b) {
            // 按照数组右边界从小到大排序
        	return Integer.compare(a[1], b[1]);
        }
    });   

    // 这里有一个坑：不能 return a[1] - b[1]，因为如果两个数组的左边界是Integer.MIN_VALUE，相减会导致超出int范围，返回错误的结果，Integer.compare的源码：
    public static int compare(int x, int y) {
        return x < y ? -1 : (x == y ? 0 : 1);
    }

2.5 最大子数组

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

法1：动态规划，O(n)时间

法2：分治，O(logn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    class Status {
        // 定义一个数组的四个状态：左边界开始的子数组最大和，右边界开始的子数组最大和，子数组最大和，数组所有元素之和
        public int lSum, rSum, mSum, iSum;
        public Status (int lSum, int rSum, int mSum, int iSum) {
            this.lSum = lSum;
            this.rSum = rSum;
            this.mSum = mSum;
            this.iSum = iSum;
        }
    }

    public int maxSubArray(int[] nums) {

        return getSum(nums, 0, nums.length - 1).mSum;
    }

    private Status getSum(int[] nums, int l, int r) {
        if (l == r) {
            return new Status(nums[l], nums[l], nums[l], nums[l]);
        }

        int mid = (l + r) / 2;
		
        // 分
        Status lStatus = getSum(nums, l, mid);
        Status rStatus = getSum(nums, mid + 1, r);
		
        // 治
        int iSum = lStatus.iSum + rStatus.iSum;
        int mSum = Math.max(Math.max(lStatus.mSum, rStatus.mSum), lStatus.rSum + rStatus.lSum);
        int lSum = Math.max(lStatus.lSum, lStatus.iSum + rStatus.lSum);
        int rSum = Math.max(rStatus.rSum, rStatus.iSum + lStatus.rSum);
        return new Status(lSum, rSum, mSum, iSum);
    }
}

2.6 最大子数组Ⅱ

  • 在2.5的基础上，添加一个可以首尾相连的条件（本质还是dp，但是很巧妙）

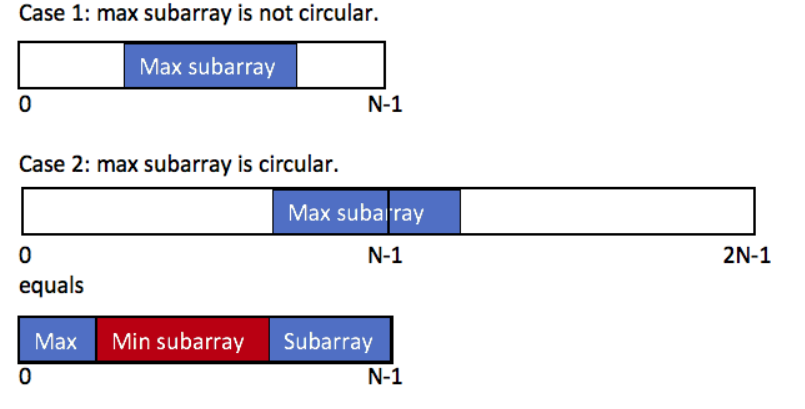
    image-20240703224831944

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int maxSubarraySumCircular(int[] A) {
    // 最大子数组和最小子数组总有一个是连续的！
    int total = 0; // 数组的总和 = maxSum + minSum
    int maxSum = A[0]; // 最大子数组和
    int curMax = 0; // 包含当前元素的最大子数组和
    int minSum = A[0]; // 最小子数组和
    int curMin = 0; // 包含当前元素的最小子数组和

    for (int a : A) {
        curMax = Math.max(curMax + a, a);
        maxSum = Math.max(maxSum, curMax);
        curMin = Math.min(curMin + a, a);
        minSum = Math.min(minSum, curMin);
        total += a;
    }
    return maxSum > 0 ? Math.max(maxSum, total - minSum) : maxSum;
}

2.7 二分查找

2.8 快速排序

  • 时间O(NlogN)，空间O(logN)~O(N),

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    private int[] fastSort(int[] nums, int l, int r) { // 升序
        if (l >= r) {
            return nums;
        }

        // int target = nums[l]; // 哨兵
        int i = l;
        int j = r;

        while (i < j) {
            while (i < j && nums[j] >= nums[l]) { // 哨兵在左，一定是从右边开始
                j--;
            }
            
            while (i < j && nums[i] <= nums[l]) {
                i++;
            }

            if (i < j) {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
            }
        }
    	
        int temp = nums[l];
        nums[l] = nums[j];
        nums[j] = temp;

        fastSort(nums, l, j-1);
        fastSort(nums, j+1, r);

        return nums;
    }

2.9 归并排序

  • 1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    void mergeSort(int[] nums, int l, int r) {
        // 终止条件
        if (l >= r) {
    		return;
        } 
        // 递归划分
        int m = (l + r) / 2;
        mergeSort(nums, l, m);
        mergeSort(nums, m + 1, r);
        
        // 合并子数组
        int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
        for (int k = l; k <= r; k++) {
            tmp[k - l] = nums[k];
        }
            
        int i = 0, j = m - l + 1;       // 两指针分别指向左/右子数组的首个元素
        for (int k = l; k <= r; k++) {  // 遍历合并左/右子数组
            if (i == m - l + 1) {
                nums[k] = tmp[j++];
            } else if (j == r - l + 1 || tmp[i] <= tmp[j]) {
                nums[k] = tmp[i++];
            } else {
                nums[k] = tmp[j++];
            }
        }
    }

2.10

  • 数组中前k个最频繁的数（hashMap + PriorityQueue）O(NlogN)

    • 更好的方法：桶排序 O(N)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> frequencyMap = new HashMap<>();
            // 统计每个数字出现的频率
            for (int num : nums) {
                frequencyMap.put(num, frequencyMap.getOrDefault(num, 0) + 1);
            }
       
            // 创建桶，桶的索引是频率，值是具有相同频率的数字列表
            List<Integer>[] buckets = new List[nums.length + 1]; // 比如1出现了3次，1就会在索引为3的桶出现
            for (int key : frequencyMap.keySet()) {
                int frequency = frequencyMap.get(key);

                if (buckets[frequency] == null) {
                    buckets[frequency] = new ArrayList<>();
                }
                buckets[frequency].add(key);
            }
        
            // 从高频到低频遍历桶，收集前 k 个频率最高的元素
            List<Integer> result = new ArrayList<>();
            for (int i = buckets.length - 1; i >= 0; i--) {
                if (buckets[i] == null) {
                    continue;
                }
                if (result.size() >= k) {
                    break;
                }
                int index = 0;
                while (result.size() < k && index < buckets[i].size()) {
                    result.add(buckets[i].get(index++));
                }
            }
            // 转换为数组返回
            return result.stream().mapToInt(i -> i).toArray();
    }

三 图

3.1 字典树

  • 典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串）。本质就是一个Node对象

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    class Trie {

        private Trie[] children;
        private boolean isEnd;

        public Trie() {
            children = new Trie[26];
            isEnd = false;
        }
        
        public void insert(String word) {
            Trie node = this;
            for (int i = 0; i < word.length(); i++) {
                char ch = word.charAt(i);
                int index = ch - 'a';
                if (node.children[index] == null) {
                    node.children[index] = new Trie();
                }
                node = node.children[index];
            }
            node.isEnd = true;
        }
        
        public boolean search(String word) {
            Trie node = searchPrefix(word);
            return node != null && node.isEnd;
        }
        
        public boolean startsWith(String prefix) {
            return searchPrefix(prefix) != null;
        }

        private Trie searchPrefix(String prefix) {
            Trie node = this;
            for (int i = 0; i < prefix.length(); i++) {
                char ch = prefix.charAt(i);
                int index = ch - 'a';
                if (node.children[index] == null) {
                    return null;
                }
                node = node.children[index];
            }
            return node;
        }
    }

四 位运算

1
2
3
4
5
n >> 1; // 向右移动一位 100110 ==> 010011，相当于/2
n & 1; // 最低一位与1 100 & 1 = 0
n | 1; // 最低一位变成1 100 | 1 = 101
	//进阶：可以用来对某一位赋值：ans |= (1 << i); //
x = x ^ num; // 异或 相同变0不同为1

4.1 快速幂

  • 快速幂法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    static long qpow(int a, int b, int mod) {
        // 求a翻倍b次，结果取模mod
        long res = 1, t = a;
        while (b > 0) {
            if ((b & 1) == 1) { // 只计算末尾是1的指数，因为任何数的0次方=1，就没必要乘了
            	res = (res * t) % mod;
            }
            b >>= 1;			// 指数位右移动：1011(2) -> 101(2)
            t = (t * t) % mod;
        }
        return res;
    }

    // 调用
    for (int i = 0; i < n; i++) {
    	res = (res + qpow(2, s[i + 1], mod) * a[i] % mod) % mod;
    }

五 其他

5.1 判断是否为质数

  • 只要把循环一直从2尝试到根号x（一个数的两个因数中，毕然有一个小于等于根号x，一个大于等于根号x）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    public static boolean isPrime1(int x){
        if(x <= 2) {
    		return true;
        }
        for(int i = 2; i <= Math.sqrt(x); i++){
            if(x % j==0){
                return false;
            }
        }
        return true;
    }